网络流学习笔记（上）

2022/11/21 学习笔记图论网络流

网络流学习笔记（上）

网络流 24 题

0.前记

学术较浅，有问题欢迎大佬们指出。

说好的打完 CSP 就开始学网络流，结果颓了快一个月才开始，打算从头到尾学一遍，但是快打 noip 了，感觉这玩意 noip 也不一定考，还是先把较为基础的东西学了吧，所以就又在“网络流学习笔记”的后面加了个“（上）”，~~noip 之后一定学一定学~~。

：

0.前记
1.网络和流
2.最大流
- 2.1 增广路
- 2.2 FF 算法
- 2.3 EK 算法
- 2.4 Dinic 算法
- 2.5 ISAP 算法
3.网络流常用模型
- 3.1 二分图最大匹配
- 3.2 最大流最小割定理
- 3.3 二者取一式问题
- 3.4 路径覆盖问题
4.费用流
- 4.1 最小费用最大流
- 4.2 二分图最大权完美匹配
5.后记

1.网络和流

本部分介绍网络流的基本概念。

网络流是什么意思，字面意思，网络和流。

网络，就是一张带权有向图；特别的，称边权为容量；额外的，有一个源点和汇点。如果在一个网络流中拥有多个源点和汇点，我们通常会建立一个超级源点和一个超级汇点，从超级源点向每一个源点连一条边，容量为正无穷，从每个汇点向超级汇点连一条边，容量也为正无穷。

流，每条边上的流不能超过它的容量，并且对于每个中继点（除了源点和汇点的所有点），流入的流量等于流出的流量。

比较抽象。不过我觉得《算法导论》的解释比较通俗易懂——“我们可以把流网络中每条有向边看做是物料的一个流通通道。每条通道有限定的容量，是物料流经该通道时的最大速率，如一条管道每小时可以流过 200 加仑的液体或一根电线可以经受 20 安培的电流。”“除了源结点和汇结点外，物料在其他结点上只是流过，并不积累或聚集。”

也就是说，在一个网络流中，每条边上所通过过的流量总和，不得大于容量。

2.最大流

本部分介绍增广路与求最大流的基础算法。

网络流中最常见的问题就是网络最大流，假设源点流出的流量可以无限多，求能够流入汇点的最大流量。

求最大流的算法有很多，一般情况下指需要掌握 EK、Dinic 和 ISAP，通常使用 Dinic 和 ISAP 算法。

至于预流推进和 HLPP 还是等到 noip 之后吧。

2.1 增广路

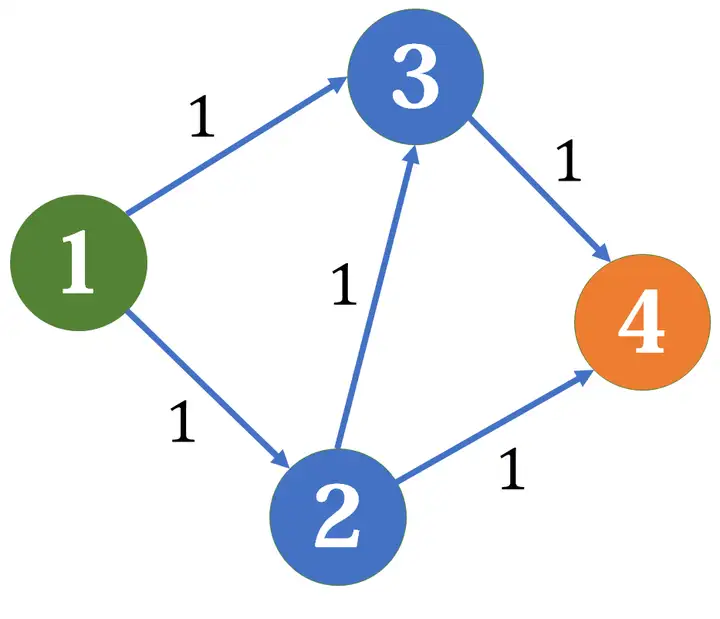
何为增广路？比方说在上图中就是一条增广路，提供 2 流量，当然我们相应的要扣除边上相应的容量，显然，只要残量网络中存在增广路，流量就可以增大，逆命题也成立。但是我们发现这样求最大流或许并不正确，比方下面这个典中典的图。

如果我们先选择了的话，我们发现残量网络中不存在增广路，此时流量为 1，但我们容易发现，如果我们选择和我们总共是可以获得 2 的流量的。

我们想，如果从流出了个流量，再从流出了个容量，是不是相当于从流出了个容量。也就是说我们通过反向边实现了撤销操作。

这时我们就要引入反向路径，即对于每条边建立一条边，容量为 0。在每次选择完增广路之后，不仅扣除掉这条边上的相应容量，还要在这条边的反向边上增加相应的容量，我喜欢把这个在反向边增加容量的操作解释为增加了可以撤销的容量。

这时我们再不断的寻找增广路，当没有增广路时，当前就是最大流。

2.2 FF 算法/Ford–Fulkerson

FF 算法实际上就是 DFS 找增广路，时间复杂度上界为，为边数，为最大流。

//B3606 [图论与代数结构 501] 网络流_1
#include<cstdio>
#include<algorithm>
#include<cstring>
using namespace std;
inline int read()
{
    int x=0,f=1;char ch=getchar();
    while(ch<'0'||ch>'9'){if(ch=='-') f=-1;ch=getchar();}
    while(ch>='0'&&ch<='9') x=x*10+ch-48,ch=getchar();
    return x*f;
}
const int MAXN=40,MAXM=410,INF=2147483647;
int n,m,s,t,to[MAXM],nxt[MAXM],head[MAXN],val[MAXM],cnt=1;long long ans;
bool vis[MAXN];
//由于要建双向边，所以边要开二倍空间；
//在建反向边的时候，我们通常将反向边的下标赋为 i^1；
//所以初始时 cnt 要为 1，还要保证反向边紧接着正向边建立；
inline void add(int x,int y,int v)//链式前向星存图；
{
    to[++cnt]=y;nxt[cnt]=head[x];
    head[x]=cnt;val[cnt]=v;return ;
}
int FF(int x,int flow)
{
    if(x==t) return flow;//到达汇点，返回当前容量；
    vis[x]=true;
    for(register int i=head[x];i;i=nxt[i])
    {
        int y=to[i];
        if(val[i]&&!vis[y])//如果剩余容量大于0并且没有访问to[i]；
        {
            int f=FF(y,min(flow,val[i]));//要取较小值；
            if(f){val[i]-=f,val[i^1]+=f;return f;}//如果找到增广路，更新并返回；
        }
    }
    return 0;
}
int main()
{
    n=read(),m=read(),s=read(),t=read();
    while(m--)
    {
        int x=read(),y=read(),c=read();
        add(x,y,c),add(y,x,0);
    }
    while(int f=FF(s,INF)) ans+=f,memset(vis,0,sizeof(vis));
    //直到没有增广路，当前已为最大流，跳出；
    printf("%lld\n",ans);return 0;
}

2.3 EK 算法/Edmonds-Karp

EK 算法实际上就是 BFS 找增广路，时间复杂度上界为，为点数，为边数。

//P3376 【模板】网络最大流
#include<cstdio>
#include<algorithm>
#include<cstring>
#include<queue>
using namespace std;
inline int read()
{
    int x=0,f=1;char ch=getchar();
    while(ch<'0'||ch>'9'){if(ch=='-') f=-1;ch=getchar();}
    while(ch>='0'&&ch<='9') x=x*10+ch-48,ch=getchar();
    return x*f;
}
const int MAXN=210,MAXM=1e4+10,INF=2147483647;
int n,m,s,t,to[MAXM],nxt[MAXM],head[MAXN],val[MAXM],last[MAXN],flow[MAXN],cnt=1;long long ans;
//last[i] 表示到 i 的那条边，flow[i] 表示到 i 时的最大流量；
inline void add(int x,int y,int v)
{
    to[++cnt]=y;nxt[cnt]=head[x];
    head[x]=cnt;val[cnt]=v;return ;
}
inline bool EK()
{
    memset(last,0,sizeof(last));//清空；
    queue <int> q;q.push(s);last[s]=-1;
    //将 s 压入队列，并且把 last[s] 赋值为 -1，这样就不会再 bfs 到 s；
    while(!q.empty())
    {
        int x=q.front();q.pop();
        if(x==t) break;//到达汇点跳出；
        for(register int i=head[x];i;i=nxt[i])
        {
            int y=to[i];
            if(val[i]&&!last[y]) last[y]=i,flow[y]=min(flow[x],val[i]),q.push(y);
            //如果剩余容量大于0并且没有访问to[i]；
        }
    }
    return last[t];//相当于返回有没有到达汇点；
}
int main()
{
    n=read(),m=read(),s=read(),t=read();
    while(m--)
    {
        int x=read(),y=read(),c=read();
        add(x,y,c),add(y,x,0);
    }
    flow[s]=INF;
    while(EK()) //直到没有增广路，当前已为最大流，跳出；
    {
        ans+=flow[t];
        for(register int i=t;i!=s;i=to[last[i]^1]) val[last[i]]-=flow[t],val[last[i]^1]+=flow[t];
        //从汇点反着回去更新；
    }
    printf("%lld\n",ans);return 0;
}

2.4 Dinic 算法

~~其实上面两个就是拿来充数的。~~

Dinic 算法就是在 FF/EK 算法上进行了大量的优化，DFS 寻找。

优化1：BFS分层

即预处理出源点和每个点之间的距离，只往层数高的方向增广，可以不走回头路，但是值得注意的是，由于增广后一些边的容量可能变为 0，所以每次 DFS 之前都要 BFS 增广。

优化2：多路增广

还可以使用多路增广，回想先前的 FF/EK 算法，我们每次只能找到一条增广路，但是如果我们在某一点找到了一条增广路，如果还剩流量未用，我们便可以在该点继续 DFS 进行多路增广。

优化3：当前弧优化

显然可证在 Dinic 中，每条路只会被增广一次，所以我们可以每次 DFS 前把数组复制一遍，每回从上一回的下一条边开始考虑增广。

时间复杂度，为点数，为边数。

//P3376 【模板】网络最大流
#include<cstdio>
#include<algorithm>
#include<cstring>
#include<queue>
using namespace std;
inline int read()
{
    int x=0,f=1;char ch=getchar();
    while(ch<'0'||ch>'9'){if(ch=='-') f=-1;ch=getchar();}
    while(ch>='0'&&ch<='9') x=x*10+ch-48,ch=getchar();
    return x*f;
}
const int MAXN=210,MAXM=1e4+10,INF=2147483647;
int n,m,s,t,to[MAXM],nxt[MAXM],head[MAXN],val[MAXM],cnt=1,dep[MAXN],cur[MAXN];long long ans;
//dep 表示层数，cur 为当前弧优化；
inline void add(int x,int y,int v)
{
    to[++cnt]=y;nxt[cnt]=head[x];
    head[x]=cnt;val[cnt]=v;return ;
}
inline bool bfs()
{
    memset(dep,-1,sizeof(dep));dep[s]=0;
    memcpy(cur,head,sizeof(head));//初始化当前弧优化；
    queue <int> q;q.push(s);
    while(!q.empty())
    {
        int x=q.front();q.pop();
        for(register int i=head[x];i;i=nxt[i])
        {
            int y=to[i];
            if(val[i]&&dep[y]==-1) dep[y]=dep[x]+1,q.push(y);
            //如果剩余容量大于0并且没有访问to[i]；
        }
    }
    return dep[t]!=-1;//相当于返回可不可以到达汇点；
}
int dfs(int x,int flow)
{
    if(x==t) return flow;//到达汇点返回；
    int rmn=flow;//剩余容量；
    for(register int i=cur[x];i&&rmn;i=nxt[i])//剩余容量为0直接跳出；
    {
        cur[x]=i;int y=to[i];//当前弧优化；
        if(val[i]&&dep[y]==dep[x]+1)//如果剩余容量大于0并且to[i]在x的下一层；
        {
            int f=dfs(y,min(rmn,val[i]));
            rmn-=f,val[i]-=f,val[i^1]+=f;
        }
    }
    return flow-rmn;//流入流量 - 剩余流量 = 实际消耗的流量；
}
int main()
{
    n=read(),m=read(),s=read(),t=read();
    while(m--)
    {
        int x=read(),y=read(),c=read();
        add(x,y,c),add(y,x,0);
    }
    while(bfs()) ans+=dfs(s,INF);
    printf("%lld\n",ans);return 0;
}

2.5 ISAP算法/Improved Shoertest Augmenting Path

ISAP 算法和 Dinic 算法有点相似，主要的优化就是只进行了一次 BFS，同时这个东西也可以进行当前弧优化。

总的执行过程就是

1. 从汇点到源点跑 BFS ，分层（注意这里是从汇点到源点）；
1. 从源点到汇点跑 DFS，和 Dinic 类似，如果说直到最后剩余流量大于 0 ，说明该点在该点以后的路上没有作用了，这时把他的深度加 1 ，ISAP 就是以此来代替每次都 BFS 的。
1. 如果在某一时刻，网络中出现了断层，即某个深度一个点都没有，那么当即停止增广（ gap 优化），否则重复 DFS。

时间复杂度上界同于 Dinic ，但由于有 gap 优化和只进行了一次 BFS，实际实现上要比 Dinic 快。

//P3376 【模板】网络最大流
#include<cstdio>
#include<algorithm>
#include<cstring>
#include<queue>
using namespace std;
inline int read()
{
    int x=0,f=1;char ch=getchar();
    while(ch<'0'||ch>'9'){if(ch=='-') f=-1;ch=getchar();}
    while(ch>='0'&&ch<='9') x=x*10+ch-48,ch=getchar();
    return x*f;
}
const int MAXN=210,MAXM=1e4+10,INF=2147483647;
int n,m,s,t,to[MAXM],nxt[MAXM],head[MAXN],val[MAXM],cnt=1,dep[MAXN],cur[MAXN],gap[MAXN];
//gap[i] 表示深度为 i 的点的个数；
long long ans;queue <int> q;
inline void add(int x,int y,int v)
{
    to[++cnt]=y,nxt[cnt]=head[x];
    head[x]=cnt,val[cnt]=v;return ;
}
inline void bfs()
{
    q.push(t);//从汇点开始；
    while(!q.empty())
    {
        int x=q.front();q.pop();gap[dep[x]]++;//统计gap；
        for(register int i=head[x];i;i=nxt[i])
        {
            int y=to[i];
            if(!dep[y]&&y!=t) dep[y]=dep[x]+1,q.push(y);
        }
    }
    return ;
}
int dfs(int x,int flow)
{
    if(x==t) return flow;
    int rmn=flow;
    for(register int i=cur[x];i&&rmn;i=nxt[i])
    {
        cur[x]=i;int y=to[i];
        if(val[i]&&dep[y]==dep[x]-1)//因为BFS是从汇点开始的，所以是 -1；
        {
            int f=dfs(y,min(rmn,val[i]));
            val[i]-=f,val[i^1]+=f,rmn-=f;
        }
    }
    if(!rmn) return flow;
    //如果没有剩余流量就返回，如果有就执行下面的操作；
    --gap[dep[x]];//先把当前这个深度点的个数 -1；
    if(!gap[dep[x]]) dep[s]=n+1;
    //如果当前这个深度没有点了，将dep[s]赋值为n+1，下一回就直接结束循环了；
    dep[x]++,gap[dep[x]]++;//深度 +1，同时要统计上；
    return flow-rmn;
}
int main()
{
    n=read(),m=read(),s=read(),t=read();
    while(m--)
    {
        int x=read(),y=read(),c=read();
        add(x,y,c),add(y,x,0);
    }
    bfs();
    while(dep[s]<n)
    {
        memcpy(cur,head,sizeof(head));
        ans+=dfs(s,INF);
    }
    printf("%lld\n",ans);return 0;
}

3.网络流常用模型

本部分介绍用网络流求二分图最大匹配，最大流最小割定理以及二者取一式和最小路径覆盖问题。

网络流的难点不在于求解，而在于建模，很有可能在一道题目看起来和网络流甚至于说图论没有任何关系，而却要通过复杂的建模来转化为网络流问题。

3.1 二分图最大匹配

先简单介绍一下二分图匹配：

二分图是指把结点集分成两部分和，使得每条边恰好一个端点在，另一个端点在。或者说，把结点进行二染色，使得同色结点不相邻。

二分图匹配分为三种，二分图最大匹配、二分图最大权完美匹配、二分图最大权匹配。

即对于一个二分图，求出包含边数最多的匹配。我们都知道可以用匈牙利算法解决，其时间复杂度为，然而我们可以使用网络流来跑的比匈牙利快。

我们可以对一个二分图增加一个源点和汇点，从源点到结点连一条容量为 1 的边，从结点到汇点连一条容量为 1 的边，把所有的原有的边看做从结点到结点的有向边，容量为 1，网络的最大流就是二分图最大匹配数。

结点到结点的有向边容量为 1 比较好理解，但为什么源点到结点和结点向汇点之间的边容量为 1 ？这里可以理解为每个点只能匹配一次，所以点可以获得的最大流量只能为 1 （@Nt_Yester）。

所以上面的步骤我们就称之为网络流的建模。

至于跑最大流，一般使用 Dinic ，可以将时间复杂度优化到 ~~但我还是喜欢用匈牙利算法~~。

//P3386 【模板】二分图最大匹配
inline bool bfs()//没有必要添加当前弧优化，事实上也不会出现多路增广；
int dfs(int x)//每次增广肯定是贡献 1 的流量；
int main()
{
    n=read(),m=read(),e=read();s=0,t=n+m+1;
    while(e--)
    {
        int u=read(),v=read();
        add(u,v+n,1),add(v+n,u,0);//把 Y 结点下标加上 n，避免重复；
    }
    for(register int i=1;i<=n;++i) add(s,i,1),add(i,s,0);//源点到 X 结点；
    for(register int i=1;i<=m;++i) add(i+n,t,1),add(t,i+n,0);//Y 结点到汇点；
    while(bfs()) ans+=dfs(s);
    printf("%d\n",ans);return 0;
}

如果需要输出合法方案，可以在最后加上

for(register int x=1;x<=n;++x)//遍历 X 结点；
    for(register int i=head[x];i;i=nxt[i])//遍历每条出边；
        if(!(i&1)&&!val[i]) printf("%d %d\n",x,to[i]);
        //如果是正向边就是连向 Y 结点的，如果权值为 0 说明这条边被增广过；

3.2 最大流最小割定理

割，就是在网络中选择若干条边，使得删去这些边后，剩下两个不联通的分别包含源点和汇点的点集，割的大小就是这些边的容量之和。

至于最大流最小割定理，就是：最小割最大流，在使用定理时其实无需证明。

最小割一般不会单独出现，所以也没什么好多说的。

3.3 两者取一式问题

二者取一式问题：形如有若干元素将他们划分到两个集合，中，对于一个元素，放到集合有的分值，放到集合有的分值，还有若干个组合，组内的所有元素同时放到或中可以获得或的分值，求分值最大。

我们将作为源点，作为汇点，先不考虑组合的情况下，可以很简单的建出下面这张图。

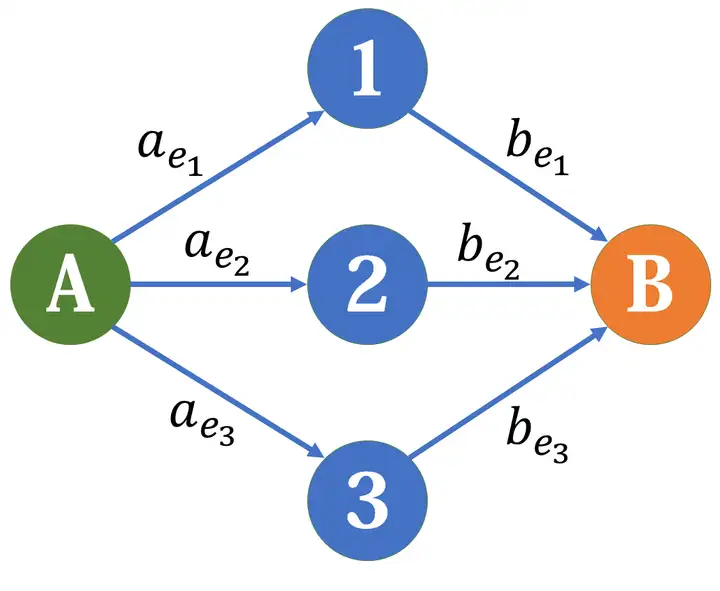
显然，此时最大的分值和为边权和最小割

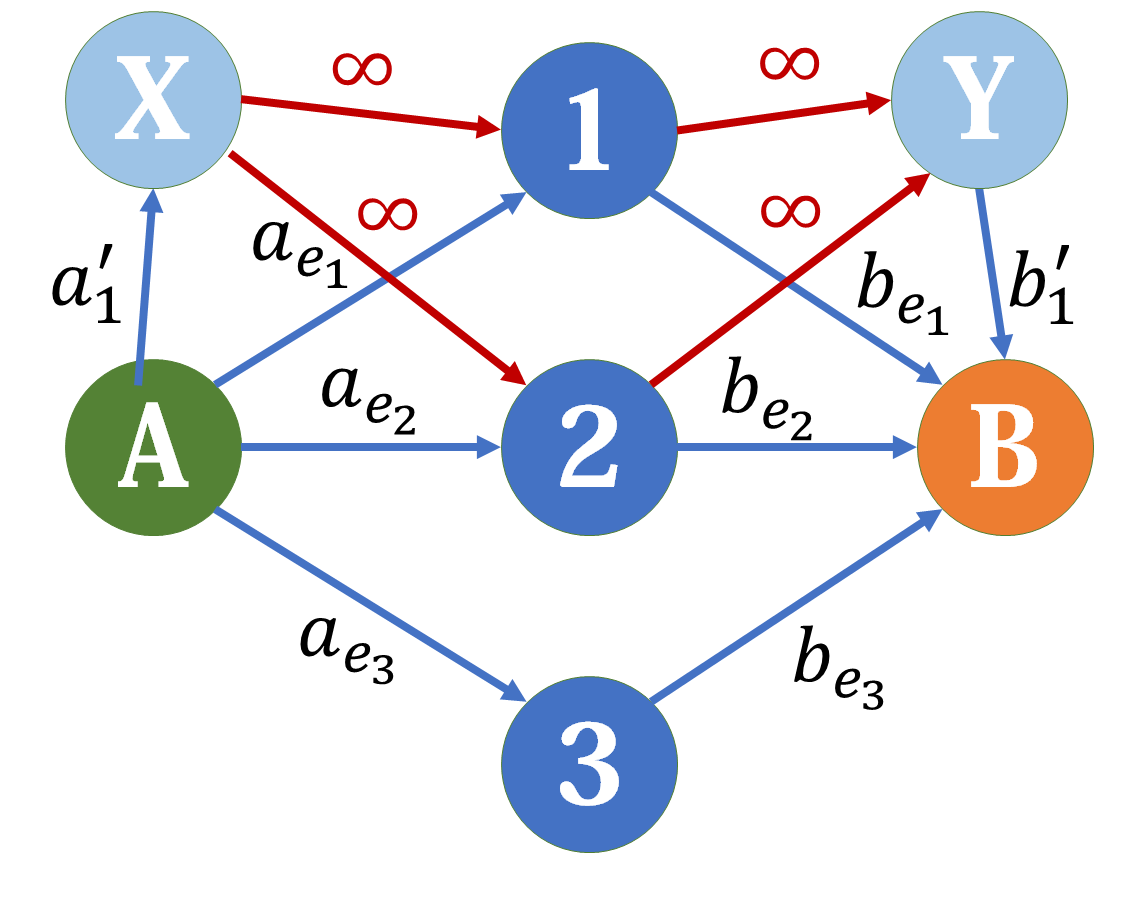
接着考虑组合的情况，我们就从向一个新的结点连一条边，容量为，从另一个新的结点向连一条边，容量为，如果我们想要让一个集合中的点都归到 A 中，我们就要使被割掉，同时我们又要保证不被割掉，那我们就要把这条边的边权赋值为正无穷，即新连一条边为，同理为。最后记录所有非无穷边权和，再减去最小割就是答案。

//P1361 小M的作物
int main()
{
    scanf("%d",&n);s=0,t=n+1;
    for(int i=1,a;i<=n;i++) scanf("%d",&a),add(0,i,a),add(i,0,0),sum+=a;
    for(int i=1,a;i<=n;i++) scanf("%d",&a),add(i,n+1,a),add(n+1,i,0),sum+=a;
    //先连上与组合无关的；
    scanf("%d",&m);
    for(int i=1,k,c1,c2,a,tot=n+1;i<=m;i++)
    {
        scanf("%d%d%d",&k,&c1,&c2);
        sum+=c1,sum+=c2;
        add(0,++tot,c1),add(tot,0,0);//新建结点 X；
        add(++tot,n+1,c2),add(n+1,tot,0);//新建结点 Y；
        while(k--)
        {
            scanf("%d",&a);
            add(tot-1,a,2e9+10),add(a,tot-1,0);//X -> e_i;
            add(a,tot,2e9+10),add(tot,a,0);//e_i -> Y;
        }
    }
    while(bfs()) ans+=(long long)dfs(s,1e9+7);
    printf("%lld\n",sum-ans);return 0;
}

3.4 路径覆盖问题

路径覆盖问题：在 DAG 中，找到一系列尽可能少的路径，使这些路径经过 DAG 上的点恰好各一次。

我们可以把原图上一个点拆开，当做两个点，对于一条边 ,改为，其中所有类似前者的点与源点相连，类似后者的点与汇点相连。每条边的容量都是 1 —— 的边容量为 1 代表一次合并，源点到每个点的边的容量为 1 可以保证只经过每个点一次。

我们有一个思路就是每个点把自己当作一条路径，每次将已有的路径首尾相连，合并成更长的路径，合并的次数越多，路径覆盖数就越小。

图片来源

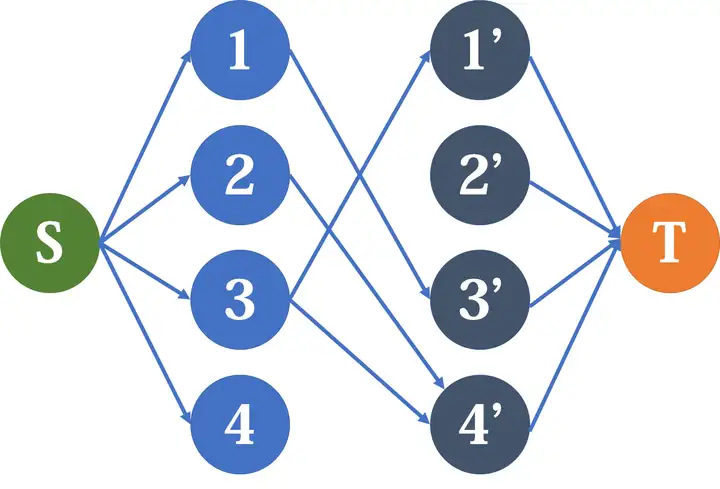
那我们就可以跑一遍最大流，其实本质上是二分图最大匹配，得到最大合并路径数，用点数减去最大路径合并数就是最小路径覆盖数。

//P2764 最小路径覆盖问题
//实质是二分图最大匹配；
int main()
{
    n=read(),m=read();s=0,t=n+n+1;
    for(register int i=1;i<=n;++i) add(s,i,1),add(i,s,0);//S -> A；
    for(register int i=1;i<=n;++i) add(i+n,t,1),add(t,i+n,0);//A' -> T;
    while(m--)
    {
        int u=read(),v=read();
        add(u,v+n,1),add(v+n,u,0);//A -> B';
    }
    while(bfs()) ans+=dfs(s);
    for(register int x=1;x<=n;++x)
        for(register int i=head[x];i;i=nxt[i])
            if(!(i&1)&&!val[i]) p[x]=to[i]-n,vis[to[i]-n]=true;
            //记录每个人的下一个，同时记录每个人有没有上一个；
    for(register int i=1;i<=n;++i)
    {
        if(!vis[i])//没有上一个，是第一个；
        {
            for(register int now=i;now;now=p[now]) printf("%d ",now);//循环输出；
            puts("");
        }
    }
    printf("%d\n",n-ans);return 0;//是 n - ans；
}

4.费用流

本部分介绍最小费用最大流和二分图最大权完美匹配。

费用流，在每条边上，除了容量，还有一个属性为单位费用，一条边上的费用等于流量单位费用。

4.1 最小费用最大流

我们知道，我们在正常的最大流中，我们并不关心增广的先后顺序，换句话说，增广的先后顺序不会对最后结果产生影响。那么我们可以每次都选择费用最少的增广，具体的，我们只需要将 EK 算法中的 BFS 替换成 SPFA（因为存在负边权，所以如果使用 Dij 需要特殊处理）。

//P3381 【模板】最小费用最大流
#include<cstdio>
#include<algorithm>
#include<cstring>
#include<queue>
using namespace std;
inline int read()
{
    int x=0,f=1;char ch=getchar();
    while(ch<'0'||ch>'9'){if(ch=='-') f=-1;ch=getchar();}
    while(ch>='0'&&ch<='9') x=x*10+ch-48,ch=getchar();
    return x*f;
}
const int MAXN=5e3+10,MAXM=1e5+10,INF=1e9+7;
int n,m,s,t,to[MAXM],nxt[MAXM],head[MAXN],val[MAXM],c[MAXM],last[MAXN],flow[MAXN],cnt=1;
long long dis[MAXN],ans,cost;
bool vis[MAXN];
inline void add(int x,int y,int v,int c)
{
    to[++cnt]=y,nxt[cnt]=head[x];
    head[x]=cnt,val[cnt]=v;
    ::c[cnt]=c;return ;//额外记录单位花费；
}
inline bool SPFA()
{
    fill(dis+1,dis+1+n,1e18);//初始化最短路；
    memset(vis,0,sizeof(vis));
    queue <int> q;q.push(s),dis[s]=0;
    while(!q.empty())//SPFA；
    {
        int x=q.front();q.pop();vis[x]=0;
        for(register int i=head[x];i;i=nxt[i])
        {
            int y=to[i];
            if(val[i]&&dis[y]>dis[x]+c[i])//当边权大于 0 才增广；
            {
                last[y]=i,flow[y]=min(flow[x],val[i]);
                dis[y]=dis[x]+c[i];
                if(!vis[y]) q.push(y),vis[y]=1;
            }
        }
    }
    return dis[t]!=1e18;//是否达到 t；
}
int main()
{
    n=read(),m=read();s=read(),t=read();
    while(m--)
    {
        int s=read(),t=read(),c=read(),w=read();
        add(s,t,c,w),add(t,s,0,-w);//这里的花费为负,代表撤销操作；
    }
    flow[s]=INF;
    while(SPFA())
    {
        ans+=flow[t],cost+=(long long)dis[t]*flow[t];
        for(register int i=t;i!=s;i=to[last[i]^1])
            val[last[i]]-=flow[t],val[last[i]^1]+=flow[t];
    }
    printf("%lld %lld\n",ans,cost);return 0;
}

我们同样可以使用 Dinic 费用流解决。

#include<cstdio>
#include<algorithm>
#include<cstring>
#include<queue>
using namespace std;
inline int read()
{
    int x=0,f=1;char ch=getchar();
    while(ch<'0'||ch>'9'){if(ch=='-') f=-1;ch=getchar();}
    while(ch>='0'&&ch<='9') x=x*10+ch-48,ch=getchar();
    return x*f;
}
const int MAXN=5e3+10,MAXM=1e5+10,INF=1e9+7;
int n,m,s,t,to[MAXM],nxt[MAXM],head[MAXN],val[MAXM],c[MAXM],cur[MAXN],cnt=1;
long long dis[MAXN],ans,cost;
bool vis[MAXN];
inline void add(int x,int y,int v,int c)
{
    to[++cnt]=y,nxt[cnt]=head[x];
    head[x]=cnt,val[cnt]=v;
    ::c[cnt]=c;return ;
}
inline bool SPFA()
{
    fill(dis+1,dis+1+n,1e18);
    memset(vis,0,sizeof(vis));
    memcpy(cur,head,sizeof(head));//当前弧优化初始化；
    queue <int> q;q.push(s),dis[s]=0;
    while(!q.empty())//SPFA；
    {
        int x=q.front();q.pop();vis[x]=0;
        for(register int i=head[x];i;i=nxt[i])
        {
            int y=to[i];
            if(val[i]&&dis[y]>dis[x]+c[i])
            {
                dis[y]=dis[x]+c[i];
                if(!vis[y]) q.push(y),vis[y]=1;
            }
        }
    }
    return dis[t]!=1e18;//能否到达 t;
}
int dfs(int x,int flow)
{
    if(x==t) return flow;
    int rmn=flow;vis[x]=1;//记录 vis;
    for(register int i=cur[x];i&&rmn;i=nxt[i])
    {
        cur[x]=i;int y=to[i];
        if(val[i]&&!vis[y]&&dis[y]==dis[x]+c[i])
        {//容量大于 0 且没有被访问过；
            int f=dfs(y,min(flow,val[i]));
            val[i]-=f,val[i^1]+=f,rmn-=f;
        }
    }
    vis[x]=0;return flow-rmn;
}
int main()
{
    n=read(),m=read();s=read(),t=read();
    while(m--)
    {
        int s=read(),t=read(),c=read(),w=read();
        add(s,t,c,w),add(t,s,0,-w);
    }
    while(SPFA()){int f=dfs(s,INF);ans+=f,cost+=(long long)dis[t]*f;}
    printf("%lld %lld\n",ans,cost);return 0;
}

4.2 二分图最大权完美匹配

二分图最大权完美匹配，即边带权，要求每个点都被匹配到，同时使权和最大。我们在二分图最大匹配中知道了如何将二分图匹配转化成网络流模型，这里只不过是多了一个边权的限制，我们可以直接转换成最小费用最大流。但是这里我们是想让“费用”最大，所以每条边的边权将其取相反数，最后的答案在取相反数即可。

就是说把原来图上的每条有向边的边权的相反数当做这条边的单位费用，其他边的费用都为 0 ，跑费用流求出最大流的相反数即为二分图最大权完美匹配。

但是值得注意的是，尽管在二分图最大匹配中网络流理论上优于匈牙利算法，但在二分图最大权完美匹配中，其时间复杂度为，是要劣于KM算法的。所以无法通过这个模板的，但还是那这个做例子，正常情况下应该不会有人卡网络流吧~~不会吧不会吧~~。

//P6577 【模板】二分图最大权完美匹配
#include<cstdio>
#include<algorithm>
#include<cstring>
#include<queue>
using namespace std;
inline int read()
{
    int x=0,f=1;char ch=getchar();
    while(ch<'0'||ch>'9'){if(ch=='-') f=-1;ch=getchar();}
    while(ch>='0'&&ch<='9') x=x*10+ch-48,ch=getchar();
    return x*f;
}
const int MAXN=1e3+10,MAXM=52e4+10,INF=1e9+7;
int n,m,s,t,to[MAXM],nxt[MAXM],head[MAXN],val[MAXM],c[MAXM],cnt=1;
long long dis[MAXN],ans,cost;bool vis[MAXN];
inline void add(int x,int y,int v,int c)
{
    to[++cnt]=y,nxt[cnt]=head[x];
    head[x]=cnt,val[cnt]=v;
    ::c[cnt]=c;return ;
}
inline bool SPFA()//基本跟上面一个意思；
{
    fill(dis,dis+2+n+n,1e18);
    fill(vis,vis+2+n+n,0);
    queue <int> q;q.push(s),dis[s]=0;
    while(!q.empty())
    {
        int x=q.front();q.pop();vis[x]=0;
        for(register int i=head[x];i;i=nxt[i])
        {
            int y=to[i];
            if(val[i]&&dis[y]>dis[x]+c[i])
            {
                dis[y]=dis[x]+c[i];
                if(!vis[y]) q.push(y),vis[y]=1;
            }
        }
    }
    return dis[t]!=1e18;
}
int dfs(int x)//二分图；
{
    if(x==t) return 1;vis[x]=1;
    for(register int i=head[x];i;i=nxt[i])
    {
        int y=to[i];
        if(val[i]&&!vis[y]&&dis[y]==dis[x]+c[i])
        {
            int f=dfs(y);
            val[i]-=f,val[i^1]+=f;
            if(f) return 1;
        }
    }
    vis[x]=0;return 0;
}
signed main()
{
    n=read(),m=read();s=0,t=n+n+1;
    for(register int i=1;i<=n;++i) add(s,i,1,0),add(i,s,0,0);
    for(register int i=n+1;i<=n+n;++i) add(i,t,1,0),add(t,i,0,0); 
    while(m--)
    {
        int y=read(),c=read(),h=read();
        add(y,c+n,1,-h),add(c+n,y,0,h);
        //这里正向边的单位费用为负，反向边的单位费用为正；
    }
    SPFA();
    while(SPFA()){int f=dfs(s);ans+=f,cost+=(long long)dis[t]*f;}
    printf("%lld\n",-cost);//相反数；
    for(register int x=n+1;x<=n+n;++x)
        for(register int i=head[x];i;i=nxt[i])
            if((i&1)&&val[i]){printf("%d ",to[i]);break;}
    return 0;
}

5.后记

说实话，觉得考 noip 之前学网络流是个错误的决定，noip 以后估计还会学剩下的东西，但也有可能不会，反正咕不咕的吧……但网络流 24 题肯定会开始写，但也不一定会写多少，反正咕不咕的吧……

参考资料：

算法竞赛入门经典（第2版）————刘汝佳
算法导论第3版————Thomas H. Cormen Charles E. Leiserson / Ronald L. Rivest Clifford Stein
算法学习笔记(28): 网络流————Pecco
究级的最大流算法：ISAP与HLPP————ONE-PIECE
算法学习笔记(5)：匈牙利算法————Pecco
算法学习笔记(29): 二者取一式问题————Pecco
算法学习笔记(30): 路径覆盖问题————Pecco
算法学习笔记(31): 最小费用最大流————Pecco
二分图的最佳完美匹配——KM算法————SixDayCoder

LOADING...

网络流学习笔记（上）