同余&逆元&CRT学习笔记

前记

upd 2022/10/9 14:36:06 : 修改了一些错误。

upd 2022/10/17 19:36:54 : 修改了 Latex 格式。

第一篇学习笔记

之前搞了好几天，后来发现忘得差不多了，又重新温习，顺便做个笔记；涉及众多式子，如果有错请指出

1.同余式

如果两个数 和 除以 后的余数相同，我们称 与 对模 同余，记作

同余式就是如上这个式子，如果换成比较简单的形式就是

同时他还有个基本性质

显然的，若 ，当且仅当 ，换言之若 ,则

这里 表示 整除 ，即 能被 整除

同余关系还具有

自反性：

对称性：，则

传递性：，且 ，则

这些性质都可以根据变形后的式子轻易得出。

2.裴蜀定理

2.1裴蜀定理

在了解了同余式的定义后，我们来看一个与之相关的定理

裴蜀定理得名于法国数学家艾蒂安·裴蜀，亦称贝祖定理。

1.裴蜀定理是指方程 有解，当且仅当 是 的倍数时，方程有整数解；

2.同时，一定存在整数 ，使 成立；

3.特别的，只有 和 互质时, 才有整数解。

极不严谨的证明：

方程两边同时除以

因为 且 ，所以 且 ，则

通俗来说就是方程左边一定为整数，所以方程右边也一定为整数，所以 一定是 的倍数

更严谨的证明方法请 bdfs。

2.2 同余式与裴蜀定理的关系

那么为什么说同余式与裴蜀定理有关呢,因为

由于我们要求的方程是与 有关的方程， 只是辅助答案且取值为任意整数，所以我们可以写成

对于这个方程我们便可用扩展欧几里得来求解

3.欧几里得&扩展欧几里得

3.1 欧几里得算法

我们自然是要先来看看欧几里得算法的

古希腊数学家欧几里得在其著作《The Elements》中最早描述了这种算法,所以被命名为欧几里得算法。

欧几里得算法又称辗转相除法，一般用来求两个数的最大公约数，即

证明：

假设

设

则 可以表示成 ( 为正整数）

则 就等于

我们知道 ，则

因此 也是 和 的最大公因数

int gcd(int a,int b){return (b)?gcd(b,a%b):a;}

#include<algorithm>
using namespace std;
int a,b;
int main(){int c=__gcd(a,b);}

3.2 扩展欧几里得

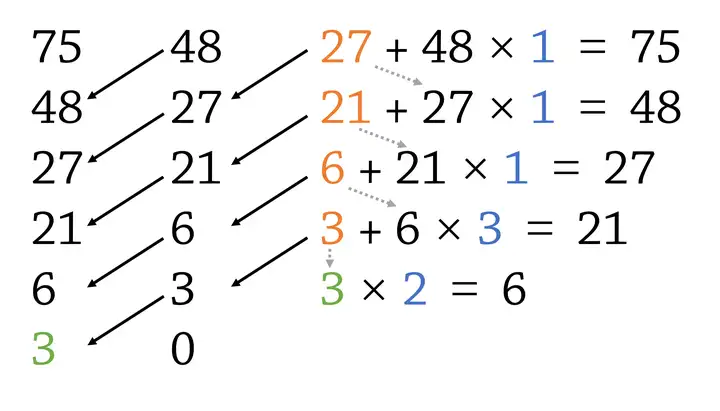
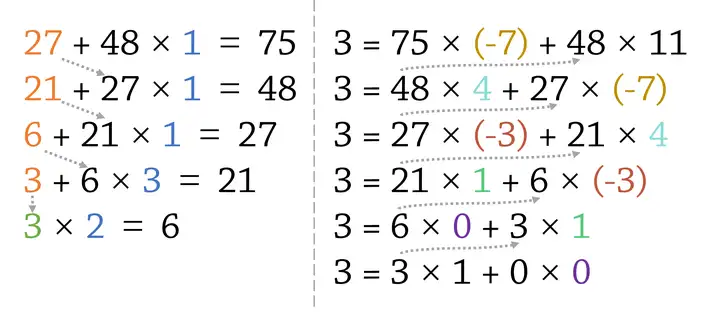
扩展欧几里得算法是欧几里得算法的扩展（废话），即我们在辗转相除的过程中，求出 的一组特解，设 为

具体的来说我们在进行辗转相除时

设当前的两个数为 （这里不是给出的 ，而是辗转相除过程中的 ）

则下一轮要递归时的两个数为

假设我们已经求出了 ，我们现在就是要利用已得出的 来推导出

因为 ，则前式可以变为

整理得

所以

那么我们的边界条件呢？

我们在辗转相除时最后当 时，我们返回的是 ，即

也就是说相当于

所以初始时 ，（其实 可以为任何数）

设求出来的特解为 ，通解即为

另外，扩展欧几里得还可以用来求逆元

//用来求不定方程 ax+by=c 的解
int x,y;
int exgcd(int a,int b,int &x,int &y)
{
    if(!b){x=1,y=0;return a;}
    int d=exgcd(b,a%b,y,x);
    y-=(a/b)*x;return d;
}

4.逆元

在数论中，如果 ，我们就说 和 在模 意义下互为乘法逆元，记作 。

实际意义即如果要在模 意义下除以一个数，就相当于乘上这个数在模 意义下的逆元

通常使用扩展欧几里得，费马小定理，和线性递推法来求乘法逆元

5.求逆元

5.1 扩展欧几里得法

我们设 为 在模 意义下的逆元,则

就相当于求

利用扩展欧几里得法求解即可

//用来求a在%p意义下的乘法逆元x
int x,y,a,p;
void exgcd(int a,int b,int &x,int &y)
{
    if(!b){x=1,y=0;return ;}
    exgcd(b,a%b,y,x),y-=(a/b)*x;return ;
}
int main()
{
  exgcd(a,p,x,y);
  x=(x%p+p)%p;
}

5.2 费马小定理

皮埃尔·德·费马于1636年发现了这个定理。在一封1640年10月18日的信中他第一次使用了上面的书写方式。在他的信中费马还提出a是一个素数的要求，但是这个要求实际上是不必要的。

费马小定理为：若 是质数，且 ，则有

至于证明，我不会

费马小定理的证明

从逆元的定义推导，可得 ，于是有

利用快速幂计算 即可

//仅适用于p为质数
int a,b,p,ans=1;
int main()
{
    b=p-2;
    while(b)
    {
        if(b&1) ans=ans*a%p;
        a=a*a%p;
        b>>=1;
    }
}

5.3 线性递推法

同时求逆元还用一种线性递推法

证明：

设 ,即

在模 意义下，有

整理得

则

即

//仅适用于p是质数
ans[1]=1;
for(int i=2;i<=n;i++)
{
    ans[i]=(-p/i*ans[p%i]);
    ans[i]=(ans[i]%p+p)%p;
}

6.中国剩余定理（CRT）

最后一趴

孙子定理是中国古代求解一次同余式组的方法。是数论中一个重要定理。又称中国余数定理。一元线性同余方程组问题最早可见于中国南北朝时期（公元5世纪）的数学著作《孙子算经》卷下第二十六题，叫做“物不知数”问题。

我们知道了如何（扩展欧几里得）求一元线性同余方程

但如果是一元线性同余方程"组"呢？

总不能求出每一个然后找公共部分吧

中国剩余定理即解决此类问题的方法

一元线性同余方程组即：

如果我们将每个方程分开看，即：

如果已经满足了 ，那么只有当 时，

同理当 时,

设有 个数，

题目上一般会给出模数两两互质的条件，继而可得当 式方程组的解时

由于模数两两互质，所以

此时求 即相当于求逆元

解得 ,则 ，

特解即为：

通解即为模 意义下所有与特解同余的数

综上得方程组的解为（这里的逆元为模 意义下的）：

for(int i=1;i<=n;i++) cin>>a[i]>>b[i],x*=a[i];
for(int i=1;i<=n;i++)
{
    int r=x/a[i];
    ans+=(b[i]*r*inv(r,a[i]))%x;
}

参考资料：

同余式-百度百科

同余方程详解-羊博士粉丝团代理团长

裴蜀定理-百度百科

扩展欧几里得算法-百度百科

算法学习笔记(8)：拓展欧几里得-Pecco

乘法逆元-百度百科

算法学习笔记(9)：逆元-Pecco

费马小定理-百度百科

费马小定理（易懂）-四年rain

孙子定理-百度百科

算法学习笔记(10): 中国剩余定理-Pecco

date：2022/10/5